8  Further topics on random variables

8.1 Transformation of random variables

8.2 Joint Probability Distributions

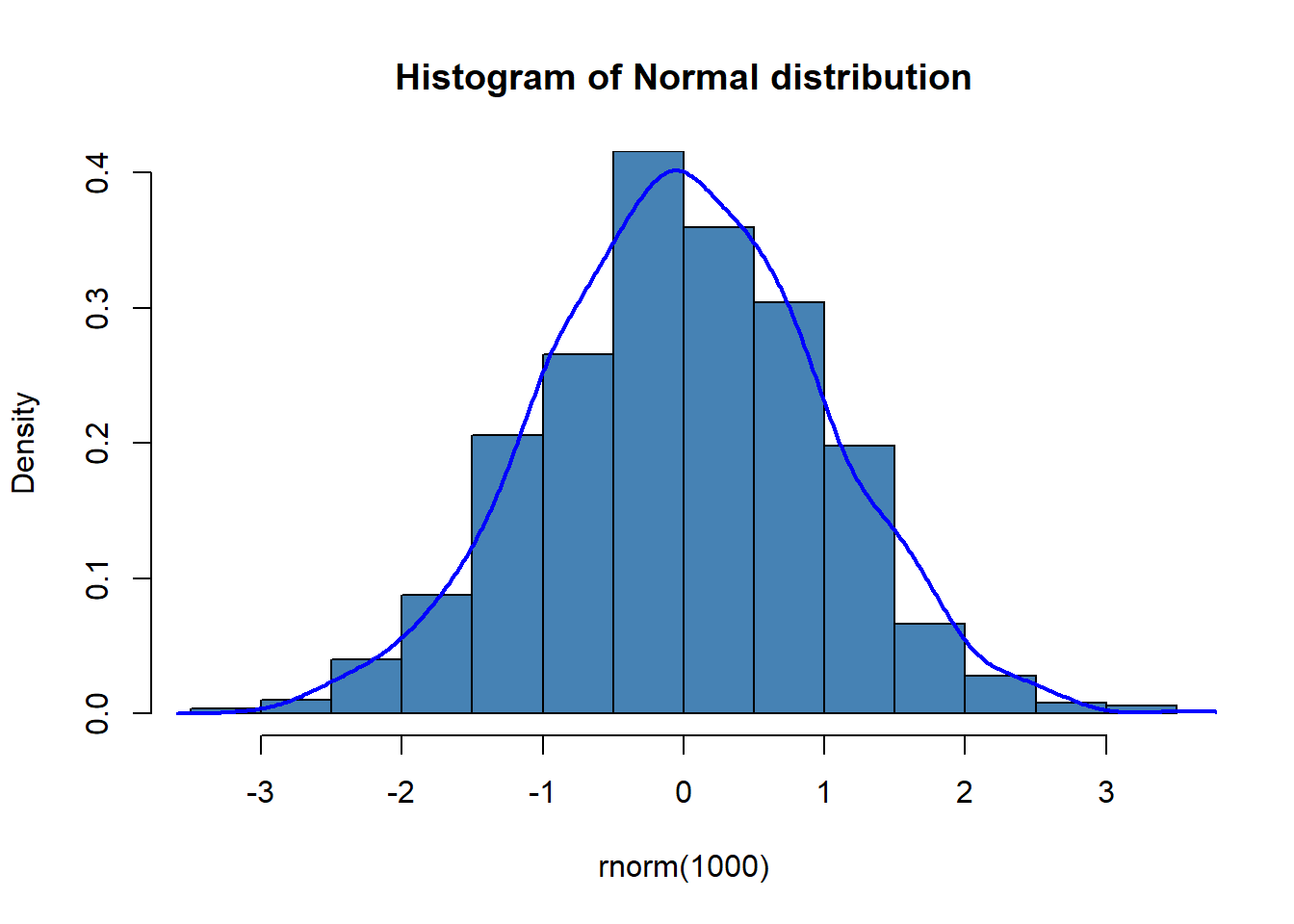
When events are happened simultaneously, to explore the relationship between two random variables we need joint probability distributions.

Definition

The function \(f(x,y)\) is said to be a joint density function of the continuous random variables \(X\) and \(Y\) if

  1. \(f(x,y)\ge0,\) for all \((x,y)\)
  2. \(\int_{-\infty}^\infty \int_{-\infty}^\infty f(x,y)\ \ dx\ \ dy=1\)
  3. \(P[(X,Y)\in A]=\int \int _A f(x,y) \ \ dx \ \ dy,\) for any region \(A\) in the plane \(xy\).
set.seed(42)

hist(rnorm(1000),freq = FALSE,ylim = c(0,.4),
     breaks = 10,col = "steelblue",main = "Histogram of Normal distribution")
lines(density(rnorm(1000)),col="blue",lwd=2)
Figure 8.1 
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
#import pandas as pd

# Generate 1000 samples
seed = 42

n_rv = np.random.normal(loc=0, scale=1, size=1000)
#print(n_rv)


#plt.clf()  # Clears the current figure

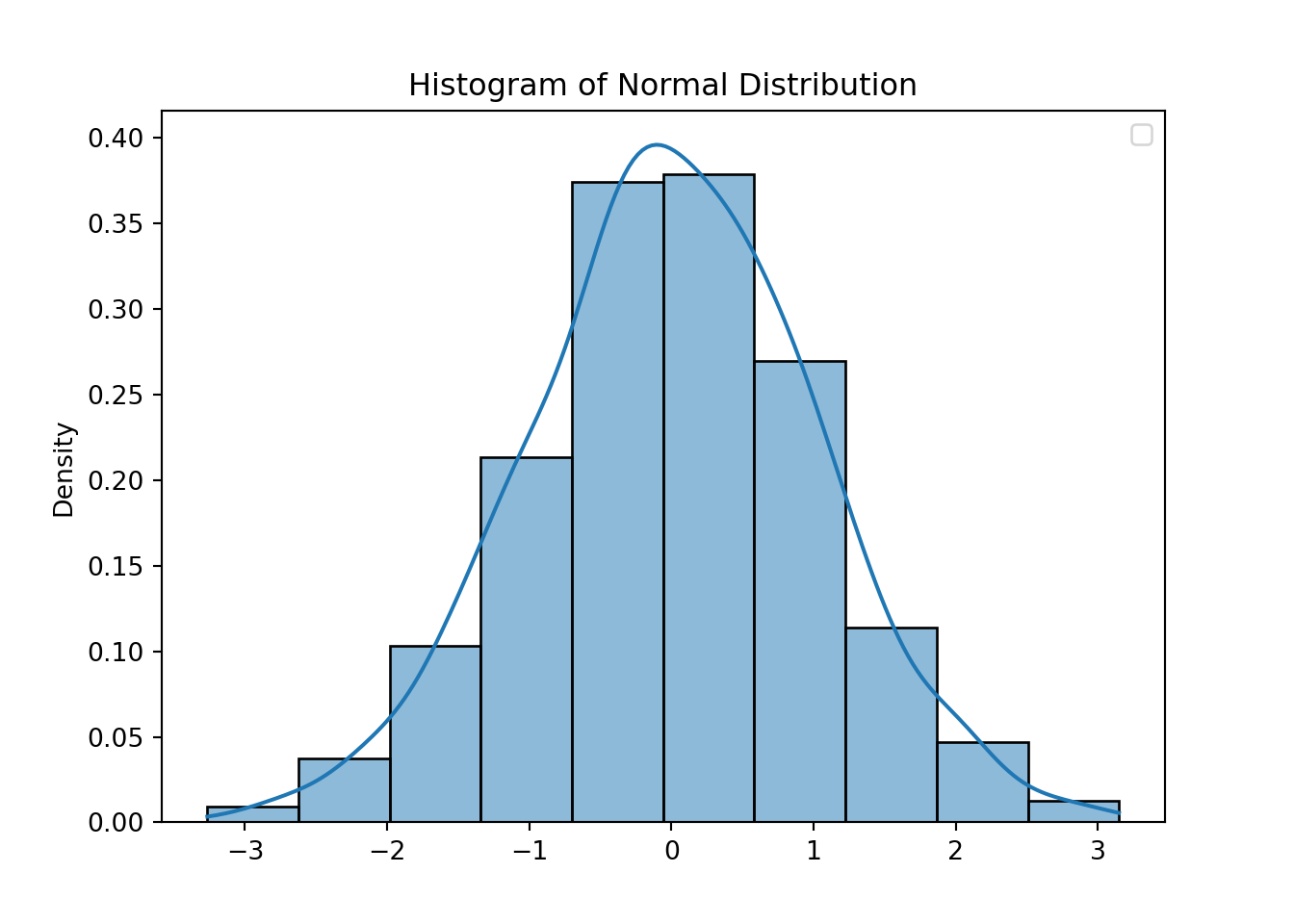
## Using `seaborn`

sns.histplot(n_rv, kde=True,stat="density",bins=10)
plt.title("Histogram of Normal Distribution")
plt.legend()
plt.show()
Figure 8.2: Histogram of Normal Distribution